Symmetrical Explained: Finding Balance In Language, Math, And Life

Have you ever stopped to truly consider the idea of things matching up perfectly? It's a concept that pops up everywhere, from the gentle curve of a leaf to the sturdy lines of a building. We often use words like "symmetrical" without fully grasping the richness behind them. But what does it truly mean for something to be symmetrical, and how does this idea shape our perception of the world around us? It's a fascinating question, really, and one that touches on everything from the words we speak to the shapes we see.

For many, the word "symmetrical" just means "the same on both sides." And while that's a good starting point, there's a lot more to it, you know? Our language, mathematics, and even the living world offer some pretty neat examples that show just how deep this concept runs. It’s not just about appearances; it’s about a fundamental arrangement of parts that creates a sense of harmony and order.

This idea of balance, of parts mirroring each other, holds a special place in how we understand structure and beauty. Whether we're looking at a piece of art, a natural wonder, or even the way words are put together, recognizing symmetry can actually open up a whole new way of seeing things. So, let's take a closer look at what "symmetrical" truly means and why it's such a significant concept, in some respects.

• Lol Superman Link
• Masa49com
• Rdxhd Movies
• Aayushi Jaiswal Hot Webseries
• Jameliz Videos

Table of Contents

• What is Symmetrical? Getting to the Core
• Symmetric vs. Symmetrical: Are They the Same?
• The Absence of Balance: Asymmetric and Dissymmetric
• Symmetrical in the World Around Us
  • Nature and Our Bodies
  • Geometric Shapes and Their Perfect Halves
  • Words That Mirror Themselves: Palindromes
• The Connection Between Rhetoric and Geometry
• How to Spot Symmetry
• Common Questions About Symmetrical
• Why Symmetry Matters

What is Symmetrical? Getting to the Core

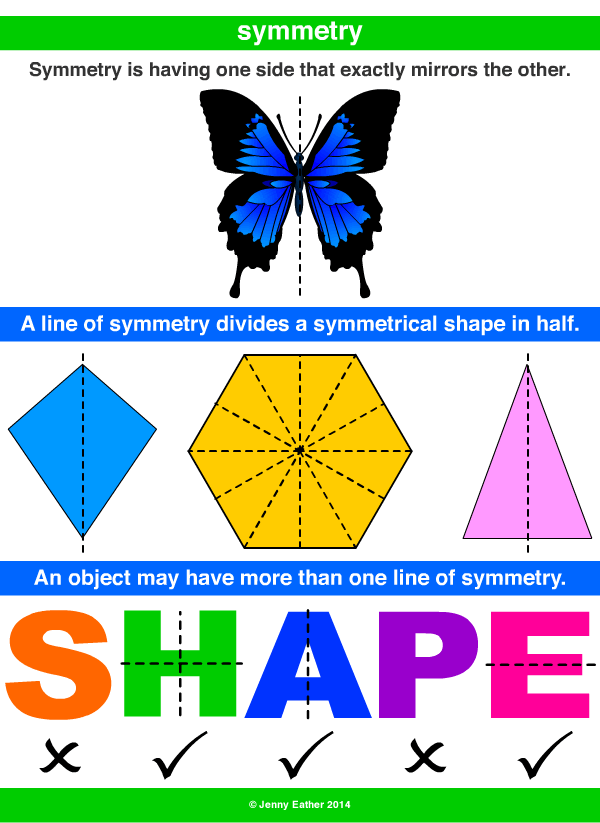
At its heart, "symmetrical" describes something that shows symmetry. This means it's identical or the same on both sides of a central dividing line or axis, you know? Imagine folding something perfectly in half, and both sides line up exactly. That's the basic idea. It can also refer to objects, designs, or forms that have parts corresponding in size, shape, and arrangement on opposite sides of a boundary or around a center. It’s about a kind of balanced arrangement of parts, really.

Think about a heart shape, for instance. If you draw a line straight down the middle, one side is a perfect match for the other. This exact matching, where one half is like a mirror image of the other, is what we mean by symmetrical. It’s a very visual concept, often tied to beauty and order in many cultures. The neat rows of perfectly symmetrical windows on an old building are a good example, showing this balanced look.

In simple terms, if something is symmetrical, one side looks just like the other. It’s about having two parts that match exactly, either when one half is like an image of the other half in a looking glass, or when parts are arranged regularly around a central point. This concept is pretty commonly seen in nature, as a matter of fact, and in things we make.

• 4k Movies Khatrimaza
• Marta Sales Sales Wikipedia
• X Hamster
• Zefoy Tiktok Likes
• Ayushi Jaiswal Ullu

Symmetric vs. Symmetrical: Are They the Same?

Now, this is a question that comes up quite a bit: what’s the difference between "symmetric" and "symmetrical"? The interesting thing is that, for most everyday uses, these two words are pretty much interchangeable. They both describe something made up of exactly similar parts facing each other or arranged around an axis. It's almost like saying "colorful" versus "colored" in some contexts; they convey a similar thought.

While "symmetric" has perhaps become a bit more common in some technical or mathematical settings lately, both words do the job of describing this balanced arrangement. So, if you're talking about a shape that has two halves which are exactly the same, you could say it's "symmetric" or "symmetrical," and people would understand you perfectly. It doesn't really matter whether this or that dictionary includes or omits one over the other; they are largely interchangeable, as I was saying.

The core meaning, having, involving, or exhibiting symmetry, holds true for both. They both refer to a balanced and even arrangement of parts. So, next time you're wondering which one to pick, remember that you’re likely safe using either one to convey the idea of something having matching halves or corresponding parts, basically. It’s pretty straightforward, you know.

The Absence of Balance: Asymmetric and Dissymmetric

If "symmetrical" means having balance and matching parts, what happens when that balance isn't there? That's where "asymmetric" and "dissymmetric" come into play. Both of these words refer to the lack of symmetry. If something is asymmetric, it simply means it doesn't have symmetry. It's unbalanced, or its parts don't mirror each other, or perhaps they don't line up neatly around a central point. Think of a lopsided drawing; that's asymmetric.

Dissymmetric, on the other hand, is a bit more specific. While it also means a lack of symmetry, it often implies a more subtle kind of asymmetry, particularly in scientific contexts like chemistry. A dissymmetric object might not have any plane of symmetry or center of inversion, but it could still be non-superimposable on its mirror image. It's a bit more nuanced than just "not symmetrical." However, for most general discussions, both asymmetric and dissymmetric point to the absence of that perfect, balanced arrangement we associate with symmetry.

So, to put it simply, if you see something that doesn't have two halves which are exactly the same, or parts that don't match up, you're looking at something that is either asymmetric or dissymmetric. It’s the opposite side of the coin, so to speak, when we talk about how things are arranged. This contrast helps us appreciate symmetry even more, I mean, when we see it.

Symmetrical in the World Around Us

The concept of symmetry isn't just a dry, academic idea; it's everywhere you look. From the grand designs of buildings to the tiny details of a snowflake, symmetry plays a huge part in how we perceive the world. It’s a very common property that makes things seem orderly and pleasing to the eye, you know. Let's explore some examples that show just how pervasive this idea truly is, as a matter of fact.

Nature and Our Bodies

Nature, in particular, is full of amazing examples of symmetry. Many animals, for instance, are bilaterally symmetrical. This means they have a longitudinal plane that divides their body into nearly identical right and left sections. Think of a butterfly, a fish, or even a human being. If you draw a line down the middle, you get two halves that are pretty much mirror images of each other. This kind of symmetry is super common in the animal kingdom, actually, and helps with movement and balance.

However, it's also worth noting that people’s bodies are never quite perfectly symmetrical. While we appear bilaterally symmetrical from the outside, if you look closely, one eye might be slightly different from the other, or one foot a tiny bit larger. These small differences add to our unique character, of course. Yet, the overall impression is one of balance and corresponding parts, which is quite remarkable.

Even a hen's egg, which might seem simple, shows a particular kind of symmetry. It's similar to an ellipse but is symmetrical about only one axis because there's a big end and a small end. The formula for a standard ellipse won't produce this exact shape, which is why it's a unique example of specific symmetry. This shows that symmetry isn't always about perfect mirror images in every direction; sometimes it's about balance along a single line, which is pretty cool.

Geometric Shapes and Their Perfect Halves

In mathematics, symmetry is a property that divides a geometrical shape into two identical halves. This is where the concept is perhaps most precisely defined. An equilateral triangle, for instance, is a classic example. You can fold it in several ways, and its halves will always line up perfectly. A rhombus is another shape that exhibits clear symmetry; its opposite sides and angles are equal, and it has lines of symmetry that divide it into matching parts.

A heart shape, as mentioned earlier, is also a prime example of a symmetrical form. If you imagine a line running vertically through its center, the left side perfectly mirrors the right. These shapes are regular in their form or arrangement of corresponding parts, which makes them inherently symmetrical. The idea of "two points in a plane such that the line segment joining them is bisected by an axis" is a more technical way to describe how symmetry works in geometry, basically.

Consider the circle, too. It’s perhaps the ultimate symmetrical shape, as it has infinite lines of symmetry passing through its center. No matter how you cut it through the middle, you get two identical halves. This kind of regular arrangement of parts is what makes these geometric figures so visually appealing and fundamental in design and architecture, you know.

Words That Mirror Themselves: Palindromes

Symmetry isn't just for shapes and bodies; it can even be found in language! A palindrome is a word, phrase, or sequence that reads the same backward as forward. This excerpt from the Oxford Dictionary of English, Third Edition, edited by a notable individual, defines it perfectly. "Madam," "level," or the phrase "A man, a plan, a canal: Panama!" are all classic examples. They show a kind of linguistic symmetry, where the structure mirrors itself, which is pretty neat.

Take the number I'm thinking of: 80808. This number is a palindrome because it reads the same backward as forward. But it's more than just a palindrome, because it can be flipped or mirrored, and it will still read the same way. This adds another layer to its symmetrical property, making it a very interesting example of how patterns can hold up even when viewed differently. It’s like a visual and numerical palindrome all rolled into one, you know.

This idea of things reading the same forward and backward, or even being able to be flipped and still make sense, highlights how symmetry can manifest in unexpected ways. It shows that the concept isn't limited to just visual balance but can apply to sequences and arrangements too. It’s a fun way to see symmetry in action, honestly, and makes you think about words differently.

The Connection Between Rhetoric and Geometry

It’s quite interesting to consider if terms from rhetoric, like ellipsis, parable, and hyperbole, have anything in common with the geometric curves ellipse, parabola, and hyperbola used in mathematics. While the words sound similar, their meanings in these different fields are, by and large, quite distinct. In rhetoric, these terms describe figures of speech, ways of using language to achieve a certain effect or emphasis, which is a very different purpose from describing shapes.

For example, an ellipsis in rhetoric means omitting words from a sentence, while a geometric ellipse is a closed curve, like a stretched circle. A parable is a simple story used to illustrate a moral or spiritual lesson, whereas a parabola is an open curve, often seen in the path of a thrown ball. Hyperbole in rhetoric is an exaggeration for effect, while a hyperbola in geometry is a curve with two branches, which is quite a different thing. So, while the names might echo each other, their applications are quite separate.

The shared sound is more of a linguistic coincidence than a deep connection in terms of meaning or symmetrical properties. The geometric curves themselves, however, do exhibit various forms of symmetry. An ellipse, for instance, is symmetrical about two axes. A parabola has one axis of symmetry. Hyperbolas also have axes of symmetry. So, while the rhetorical terms don't directly relate to symmetry, the geometric shapes they share names with certainly do, which is an interesting point, actually.

How to Spot Symmetry

Recognizing symmetry is often pretty straightforward once you know what to look for. The easiest way to spot it is to imagine a line, called an axis, running through the middle of an object or image. If one side of that line is a perfect mirror image of the other, then you've found symmetry. This is what we call reflectional or bilateral symmetry, and it's perhaps the most common type we encounter, as a matter of fact.

Another way to identify symmetry is to see if an object looks the same after being rotated around a central point. This is rotational symmetry. Think of a star or a wheel; if you spin it a bit, it still looks the same. Then there's translational symmetry, where a pattern repeats itself by sliding it along a line, like in a repeating wallpaper design. Each type shows a different kind of balanced arrangement, you know.

Practicing by looking at everyday objects can really help. Pick up a leaf, look at your own face in a mirror, or examine a building. You'll start to notice how often things are designed or occur with this balanced quality. It’s about looking for those corresponding parts that are the same in size and shape, whether they’re facing each other or arranged around a center. It becomes second nature after a while, honestly.

Common Questions About Symmetrical

What is the appropriate usage of symmetrical and symmetric?

As we've discussed, "symmetrical" and "symmetric" are largely interchangeable for most purposes, especially when referring to the geometrical adjectival definition of both terms. While "symmetric" has perhaps gained a bit more traction in some technical fields recently, you can generally use either word to describe something that has matching parts or is balanced around an axis. Both convey the idea of exhibiting symmetry, so you're good to go with either, you know.

How do you use symmetrical in a sentence?

Using "symmetrical" in a sentence is quite simple. You'd use it just like any other adjective to describe a noun that possesses symmetry. For example, you could say, "The architect designed a perfectly symmetrical facade for the building," or "The butterfly's wings were beautifully symmetrical." It simply means "having, involving, or exhibiting symmetry," so you just apply it to whatever object or design shows that balanced quality, basically.

Are people’s bodies perfectly symmetrical?

No, people’s bodies are never quite perfectly symmetrical. While we are generally considered bilaterally symmetrical, meaning we have a right and left side that are roughly mirror images, if you look closely, you’ll find subtle differences. One hand might be slightly larger, or facial features might not align perfectly. These slight variations are completely normal and contribute to each person's unique appearance. So, while the overall design suggests symmetry, the reality is a bit more nuanced, you know.

Why Symmetry Matters

The concept of "symmetrical" goes beyond just a definition; it touches on how we perceive order, beauty, and even logic in the world. From the grand designs of ancient architecture to the delicate structure of a snowflake, symmetry often brings a sense of calm and visual appeal. It’s a fundamental principle that helps us organize and understand complex forms, which is pretty significant.

Whether you're exploring the precision of mathematical shapes, appreciating the natural balance in a forest, or just noticing the even arrangement of windows on a house, the idea of symmetry is always at play. It reminds us that there's often an underlying order to things, even in what might seem chaotic at first glance. It's a lens through which we can better appreciate the intricate details of our surroundings, you know.

So, the next time you see something that just looks "right" or "balanced," take a moment to consider why. Chances are, it's exhibiting some form of symmetry. It’s a simple concept with profound implications for how we understand design, nature, and even our own bodies. Keep an eye out for it; you might be surprised at how much you start to notice. You can Learn more about balance and design on our site, and perhaps explore other fascinating patterns in the world, too it's almost everywhere.